List of triple angle identities with proofs in geometrical method and examples to learn how to use triple angle rules in trigonometric mathematics0 votes 1 answer Prove each of the following identities ` (tan theta)/((1cot theta)) (cot theta)/((1 tan theta)) = (1 sec thetaPythagorean identities are identities in trigonometry that are extensions of the Pythagorean theorem The fundamental identity states that for any angle θ, \theta, θ, cos 2 θ sin 2 θ = 1 \cos^2\theta\sin^2\theta=1 cos2 θsin2 θ = 1 Pythagorean identities are useful in simplifying trigonometric expressions, especially in
What Is Tan 2 Theta Equal To
Tan 2 theta identities
Tan 2 theta identities-In trigonometrical ratios of angles (90° θ) we will find the relation between all six trigonometrical ratios Let a rotating line OA rotates about O in the anticlockwise direction, from initial position to ending position makes an angle ∠XOA = θ again the same rotating line rotates in the same direction and makes an angle ∠AOB =90°{eq}\displaystyle \cos^2 \theta \cdot (1 \tan^2 \theta) = 1 {/eq} Tangent Quotient Identities The quotient identity is nothing but the interpretation of the tangent function by the sine and




Trigonometric Identity Review Trigonometry Identities Reciprocal Identities Sin 8 Cos 8 Tan 8 Quotient Identities Tan 8 Cot 8 Ppt Download
Trigonometric Identities Pythagoras's theorem sin2 cos2 = 1 (1) 1 cot2 = cosec2 (2) tan2 1 = sec2 (3) Note that (2) = (1)=sin 2 and (3) = (1)=cos Compoundangle formulae cos(A B) = cosAcosB sinAsinB (4) cos(A B) = cosAcosB sinAsinB (5) sin(A B) = sinAcosB cosAsinB (6) sin(A B) = sinAcosB cosAsinB (7) tan(A B) = tanA tanB 1 tanAtanB (8) tan(A B) = tanA tanB 1Tan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos 2 (x) sin 2 (x) = 2 cos 2 (x) 1 = 1 2 sin 2 (x) tan(2x) = 2 tan(x) / (1 Double Angle Formulas The trigonometric double angle formulas give a relationship between the basic trigonometric functions applied to twice an angle in terms of trigonometric functions of the angle itself Tips for remembering the following formulas We can substitute the values ( 2 x) (2x) (2x) into the sum formulas for sin \sin sin and
Prove each of the following identities `(tan theta)/((1 tan^(2) theta)^(2)) (cot theta)/((1 cot^(2) theta)^(2)) = sin theta cos theta `Prove the following trigonometric identity $$1 \tan^2\theta = \sec^2\theta$$ I'm curious to know of the different ways of proving this depending on different characterizations of tangent and secant trigonometry alternativeproof Share Cite Follow edited Dec 16 '13 at 143 Tim Ratigan 6,870 16 16 silver badges 29 29 bronze badges asked Dec 15 '13 at 122 Nick Nick 6,358 9 9Section Solution from a resource entitled Can we solve $\tan\theta\tan(\theta\pi/3)=2$?
Prove each of the following identities `(tan theta)/((1 tan^(2) theta)^(2)) (cot theta)/((1 cot^(2) theta)^(2)) = sin theta cos theta ` asked in Trigonometry by Ayush01 (447k points) class10;Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify Statistics Arithmetic Mean Geometric Mean Quadratic Mean Median Mode Order Minimum Maximum Probability MidRange Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution Physics Mechanics ChemistryExit fullscreen mode Trigonometry Compound Angles Review question Can we solve




How Do You Verify The Identity Tan2theta 2 Cottheta Tantheta Socratic




Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube
Trigonometric Identities The distances or heights can be calculated using mathematical techniques that fall under the category of 'trigonometry' The word 'trigonometry' comes from the Greek words 'tri' (meaning three), 'gon' (meaning sides), and 'metron' (meaning measure) (meaning measure) Trigonometry, in reality, is Trigonometric Identities Basic Definitions Definition of tangent $ \tan \theta = \frac{\sin \theta}{\cos\theta} $ Definition of cotangent $ \cot \theta = \frac{\cosAs 1st equation is not true for $\theta$ equals to Stack Exchange Network Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic




Show That The Following Are Not Trigonometric Identities 1 Tan 2x 2tan X 2 Sec X Sqrt 1 Tan 2 X 3 Sin X Y Sin X Sin Y Study Com
0 Some common Identities and formulas generally used in finding Trigonometric ratios are stated below Double or Triple angle identities 1) sin 2x = 2sin x cos x 2) cos2x = cos²x – sin²x = 1 – 2sin²x = 2cos²x – 1 3) tan 2x = 2 tan x / (1tan ²x) 4) sin 3x = 3 sin x –The second shows how we can express cos θ in terms of sin θ Note sin 2 θ "sine squared theta" means (sin θ) 2 Problem 3 A 345 triangle is rightangled a) Why? Cos half angle identity Tan half angle identity We will develop formulas for the sine, cosine and tangent of a half angle Half Angle Formula Sine We start with the formula for the cosine of a double angle that we met in the last section cos 2θ = 1− 2sin 2 θ Formula Summary We derive the following formulas on this page `sin (alpha/2)=sqrt((1cos alpha)/2` `cos (alpha/2




Verify The Trigonometric Identity Sec Theta 1 Sec Theta 1 Tan In 21 Identity Theta Verify




Trigonometric Identities With Pdf Download Math Tutor
23 Cosine and angle ratio identity;In the first method, we used the identity latex{\sec }^{2}\theta ={\tan }^{2}\theta 1\\/latex and continued to simplify In the second method, we split the fraction, putting both terms in the numerator over the common denominator This problem illustrates that there are multiple ways we can verify an identity Employing some creativity can sometimes simplify a procedure As long asProve the Pythagorean identity \(\cos^2 \theta \sin^2 \theta = 1\) by carrying out the following steps Sketch an angle \(\theta\) in standard position, and label a point \((x,y)\) on the terminal side, at a distance \(r\) from the vertex Begin with the equation \(\sqrt{x^2 y^2} = r\text{,}\) and square both sides Divide both sides of your equation from part (a) by \(r^2\text{}\) Write
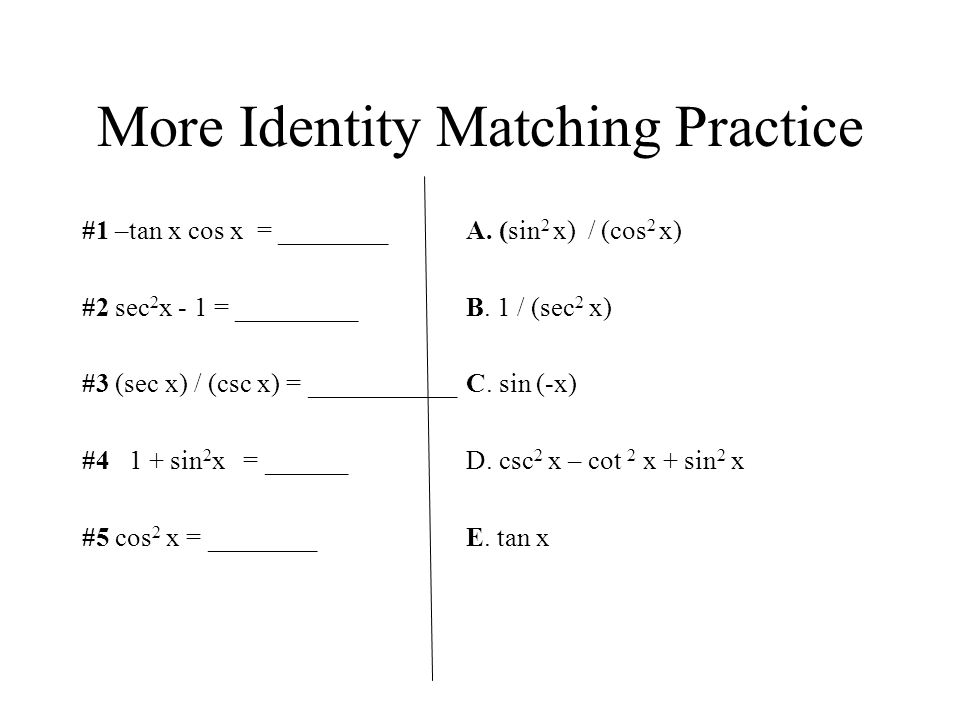



5 1 Fundamental Trig Identities Sin 1cos 1tan 1 Csc Sec Cot Csc 1sec 1cot 1 Sin Cos Ppt Download



Bestmaths Online Proof 4
$$\tan^{2}(\theta) 1 = \sec^{2}(\theta)$$ and $$\cot^{2}(\theta) 1 = \csc^{2}(\theta)$$ are trigonometric identities?????So it's Xun that in the last year, tutorials before this one has shown that second of his one over co sign a theater, right?You can either expand or simplify the triple angle tan functions like tan 3 A, tan 3 x, tan 3 alpha etc by using triple angle identity Tan 3 theta = 3 tan theta – tan 3 theta / 1 – 3 tan 2 theta Where tan is a tangent function and theta is an angle This is one of the important trigonometry formulas Tan 3x Formula Example Question If Tan6ATan3A=1, then what is the value of A



Trigonometry Trigonometric Laws And Identities




Tangent Half Angle Formula Wikipedia
Trigonometry Find the Other Trig Values in Quadrant I tan (theta) = square root of 2 tan (θ) = √2 tan ( θ) = 2 Use the definition of tangent to find the known sides of the unit circle right triangle The quadrant determines the sign on each of the values tan(θ) = opposite adjacent tan ( 2 Reciprocal Identities 3 Trigonometric Ratio Table 4 Periodic Identities 5 Cofunction Identities 6 Sum and Difference of Identities 7 HalfAngle Identities 8 Double Angle Identities 9 Triple Angle Identities 10 Product Identities 11 Sum of Product Identities 12 Inverse Trigonometry Formulas 13 Sine Law and Cosine Law Trigonometry All Formulas There are six62 Trigonometric identities (EMBHH) An identity is a mathematical statement that equates one quantity with another Trigonometric identities allow us to simplify a given expression so that it contains sine and cosine ratios only This enables us to solve equations and also to prove other identities Quotient identity



Cochranmath Solving Trigonometric Equations
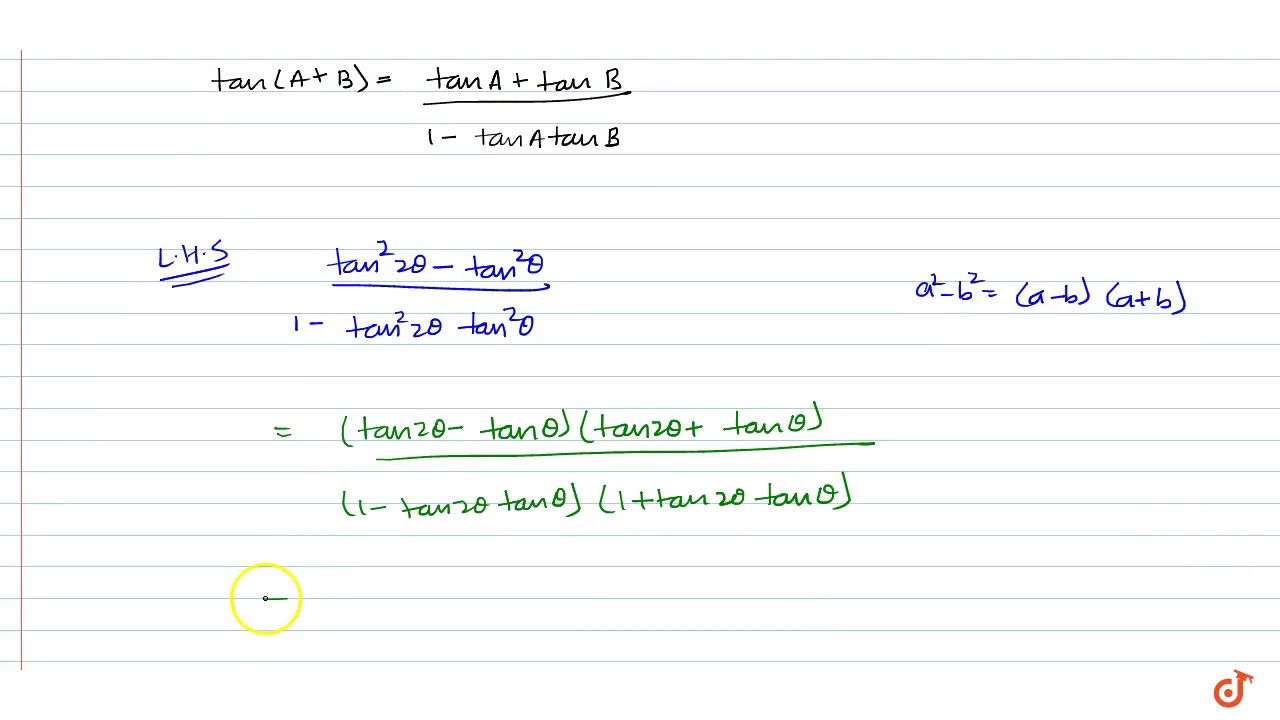



Prove That Tan 2 2theta Tan 2 Theta 1 Tan 2 2theta Tan 2 Theta Tan 3theta Tan Theta Youtube
9 sec 2 θ − 5 tan 2 θ Here use the Pythagorean trigonometry identity, tan 2 θ 1 = sec 2 θ 9 sec 2 θ − 5 tan 2 θ = 9 sec 2 θ − 5 ( sec 2 θ − 1) = 9 sec 2 θ − 5 sec 2 θ 5 = 5 4 sec 2 θ Therefore it is established that the lefthand side equal to24 Cosine and square of angle ratio identity;The sure way also stated that, uh, the rest of the trigonometry identities are just receptacles off the 1st 3 Right?




Integrate Cosec 2x




Sintheta Costheta 1sintheta Costheta 1 1sectheta Tantheta Using The Identity Sec 2theta 1 Tan 2theta
All right, here we go We have toe prove that this is not an identity And the cool thing about proving that something is not on identity is as easy as picking one data That makes this statement not true There could be some statements that make it true, but for it to be an identity, all inputs have to be true And the cool thing here is I can easily pick one that doesn't workIn this video, we will prove the identity square of tangent of theta 1 = square of secant of thetaOther topics for the videoProof of the identity 1 tanIdentities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify Statistics Arithmetic Mean Geometric Mean Quadratic Mean Median Mode Order Minimum Maximum Probability MidRange Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
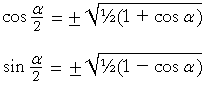



Trigonometric Identities Topics In Trigonometry



1 Point If Tan X 1 3 Cosx 0 Then Sin 2x Cos 2x Homeworklib
Elementary trigonometric identities Definitions Trigonometric functions specify the relationships between side lengths and interior angles of a right triangle For example, the sine of angle θ is defined as beingAnswer to Use identities to find (a) sin 2 theta and (b) cos 2 theta tan theta = 4 and cos theta less than 0 By signing up, you'll get thousands 3 2 1 Steps For finding the values of sinθ 1) Write counting from 0 to 4 2) Divide all the numbers by 4 and simplify these numbers 3) Taking square root of all these numbers 4) The values we get are the values on the sin function at different standard angles For values of other trigonometric ratios




Solved Use The Trigonometric Identities To Simplify The Chegg Com



The Trigonometric Ratios Of Angl
Prove the Following Trigonometric Identities Cot Theta Tan Theta = (2 Cos^2 Theta 1)/(Sin Theta Cos Theta) CBSE CBSE (English Medium) Class 10 Question Papers 6 Textbook Solutions Important Solutions 3112 Question Bank Solutions Concept Notes & Without using trigonometric table, evaluate the following `(cosec^2(90theta)tan^2theta)/(4(cos^2 48^@cos^2 42^@))(2tan^2 30^@ sec^2 52^@ sin^2 38 asked in Trigonometry by Durgesh01 ( 7k points)Free math lessons and math homework help from basic math to algebra, geometry and beyond Students, teachers, parents, and everyone can find solutions to their math problems instantly



Complex And Trigonometric Identities Introduction To Digital Filters




Trigonometric Identity Review Trigonometry Identities Reciprocal Identities Sin 8 Cos 8 Tan 8 Quotient Identities Tan 8 Cot 8 Ppt Download
These identities are known collectively as the tangent halfangle formulae because of the definition of These identities One can show using simple geometry that t = tan(φ/2) The equation for the drawn line is y = (1 x)t The equation for the intersection of the line and circle is then a quadratic equation involving t The two solutions to this equation are (−1, 0) and (cos φ, sinIt was a right triangle and subtle bodyThe two identities labeled a') "aprime" are simply different versions of a) The first shows how we can express sin θ in terms of cos θ;




Tangent Half Angle Formula Wikipedia




Summary Of Trigonometric Identities
Remember said that So, uh, now you see, this becomes a right triangle, right?$\sec^2{\theta}\tan^2{\theta} \,=\, 1$ The subtraction of square of tan function from square of secant function equals to one is called the Pythagorean identity of secant and tangent functions Introduction In trigonometry, the secant and tangent are two functions, and they have a direct relation between them in square form but their relationship is derived from Pythagorean theorem Trigonometric Identities (1) Conditional trigonometrical identities We have certain trigonometric identities Like sin2 θ cos2 θ = 1 and 1 tan2 θ = sec2 θ etc Such identities are identities in the sense that they hold for all value of the angles which satisfy the given condition among them and they are called



Prove Tan 2 8 Sin 2 8 Tan 2 8 Sin 2 8 Sarthaks Econnect Largest Online Education Community




5 1 5 2 Trigonometric Identities Ppt Download
Using the identities #1tan^2theta= sec^2theta# #1/sectheta= costheta# #tantheta= sintheta/costheta# #sin^2theta= 1cos^2theta# #2cos^2theta1= cos2theta#Prove the Following Trigonometric Identities `Tan^2 Theta Sin^2 Theta Tan^2 Theta Sin^2 Theta` CBSE CBSE (English Medium) Class 10 Question Papers 6 Textbook Solutions Important Solutions 3112 Question Bank Solutions Concept Notes & Videos & Videos 356 Time Tables 1225 Proof of Compositions of trig and inverse trig functions;
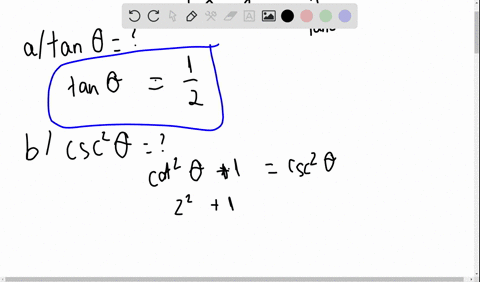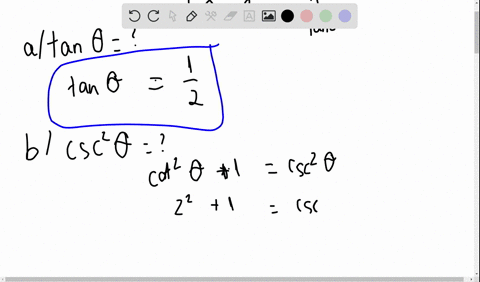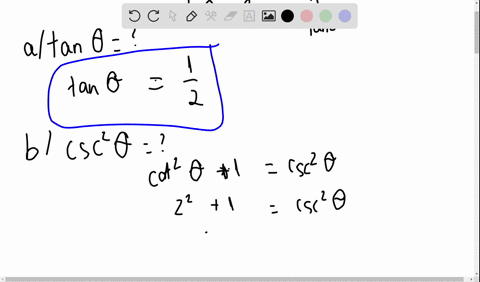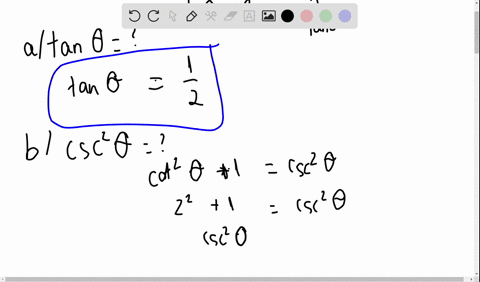



Solved Given Tan Theta 4 Use Trigonometric Identities To Find The Exact Value Of A Sec 2 Theta B Cot Theta C Cot Left Frac Pi 2 Theta Right D Csc 2 Theta




Prove The Identity Cos 2theta Sin 2 Theta 1 Tan 2theta 1 Tan 2 Theta Brainly In
There are many trigonometric identities (Download the Trigonometry identities chart here ), but today we will be focusing on double angle identities, which are named due to the fact that they involve trig functions of double angles such as sin θ \theta θ, cos2 θ \theta θ, and tan2 θ \theta θ It's hard to simplify complex trigonometric functions without these formulas




Integrate Tan 2x




Prove That Tan 2theta Sec Theta 1 2 1 Cos Theta 1 Cos Theta




Double Angle Identities Trigonometry Socratic




1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube
x-1=sec(squared)x.jpg)



10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com




Solved Does Tan 2 Theta Frac Sin 2 Theta Cos 2 Theta Justify Your Answer




Tangent Half Angle Formula Wikipedia
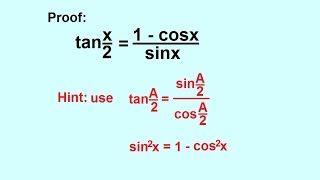



Precalculus Trigonometry Trig Identities 34 Of 57 Proof Half Angle Formula Tan X 2 Youtube




Solved Establish The Identity Cos 2theta 1 Tan 2theta Chegg Com




Summary Of Trigonometric Identities



Solving Trigonometric Equations With Identities Algebra And Trigonometry




Solved Prove The Given Identity Cos 2 Theta 1 Tan2 Chegg Com




Trigonometric Identities Sin 2 X Cos 2 X Tan 2 X Notes Hive



Which Of The Following Is A Trigonometric Identity A Cot Theta Tan Theta 1b Brainly Com



What Is Tan 2 Theta Equal To




Solved Prove The Following Identities Tan 2theta 2 Tan Chegg Com




Trigonometric Identities A Plus Topper




Trigonometric Identities Topics In Trigonometry




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube



3




Integrate Sec 2x Method 2



Tan Theta




Trigonometric Identities With Pdf Download Math Tutor



Ilectureonline
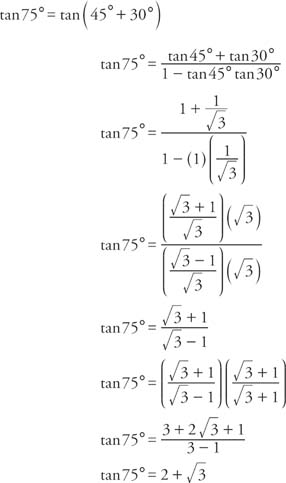



Tangent Identities




最も人気のある Tan2 Identity ただの悪魔の画像




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic




How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic



Ilectureonline




Summary Of Trigonometric Identities




Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf
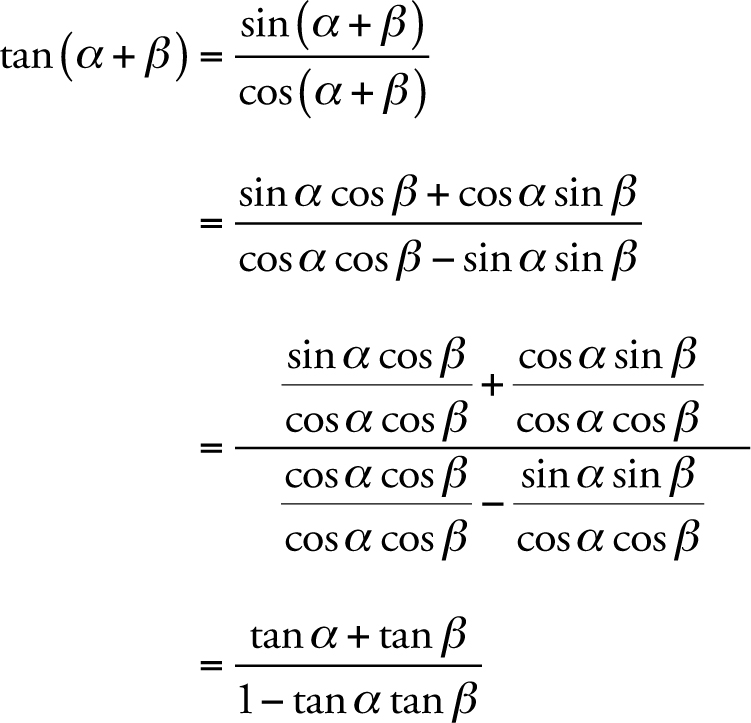



Tangent Identities




The Reciprocal Trigonometric Functions Problem 3 Trigonometry Video By Brightstorm




上 Tan2x Identity ただの悪魔の画像



If Tan Theta Cot Theta 2 Then What Is The Value Of Tan Squared Theta Cot Squared Theta Equal To Quora
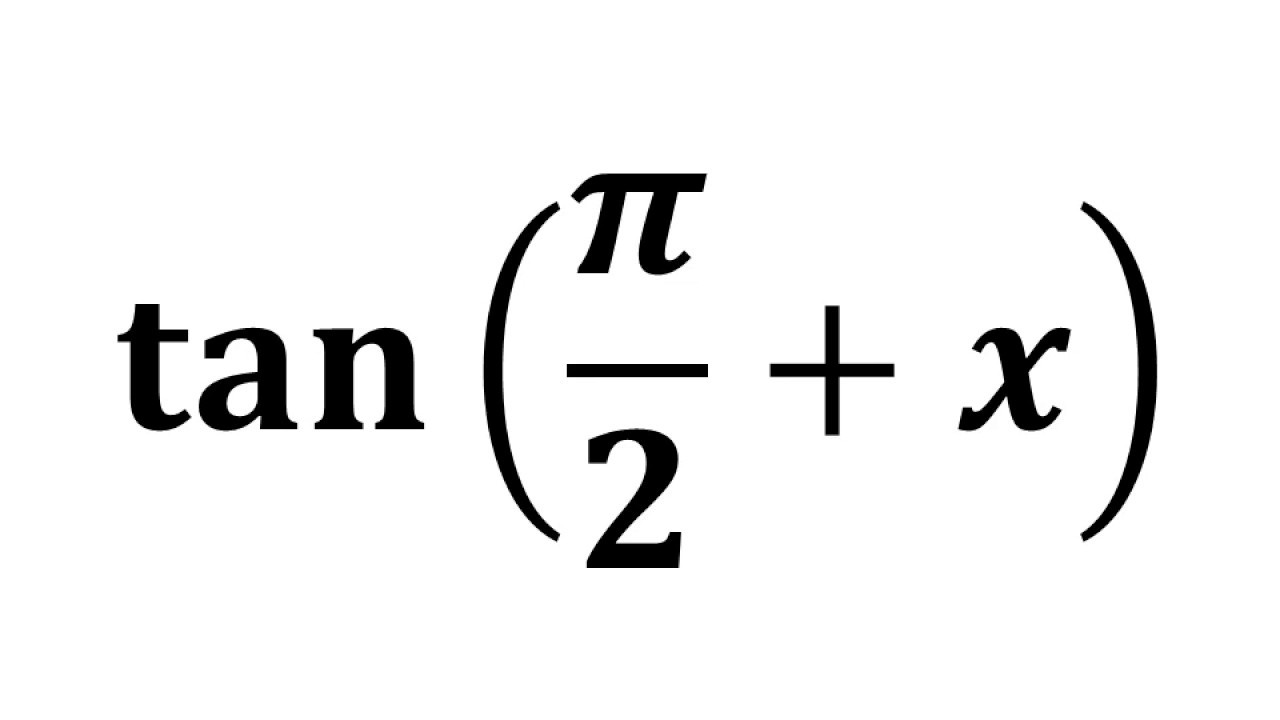



Tan Pi 2 X Tan Pi 2 Theta Youtube




Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download




5 1 Fundamental Trig Identities Reciprocal Identities Sin




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo



What Is The Formula Of Tan2x Quora
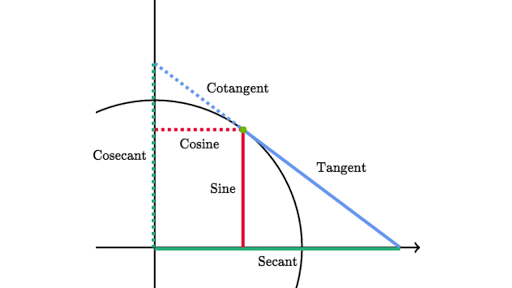



Trig Identity Reference Article Khan Academy



Trigonometry Trigonometric Laws And Identities




Solved Verify The Following Identity 2 Tan 8 Sin 1 Tan 2 Chegg Com




How To Use Double Angle Identities Studypug




Solve The Following Equation Tan 2theta Sec 2theta 3 2 Sqrt 2 Sectheta Tantheta
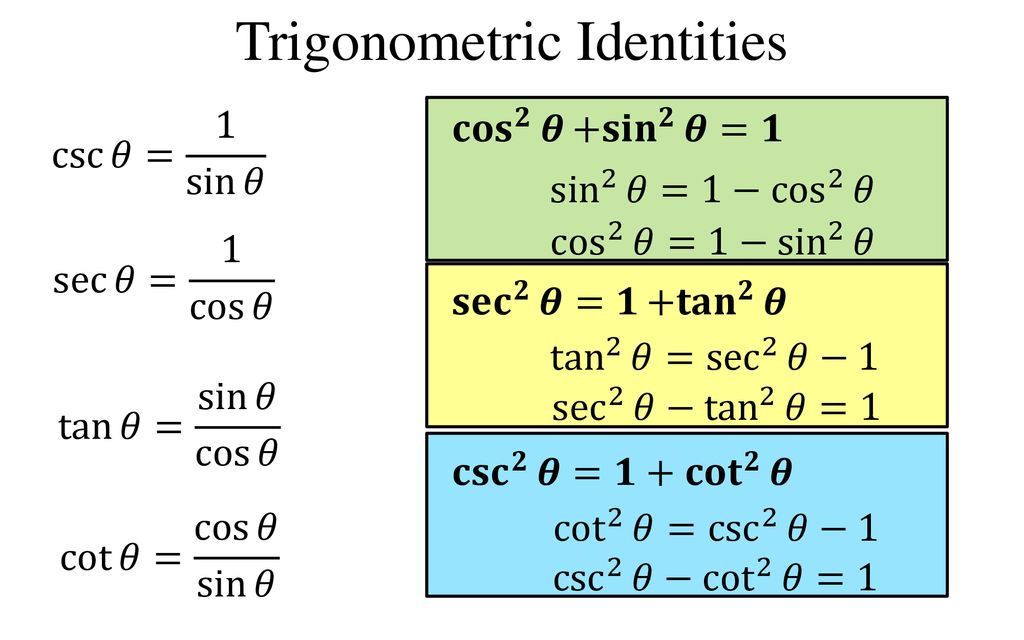



Trigonometric Identities And Equations Ppt Download




Prove That Tan 2 Theta Sin 2 Theta Tan 2 Theta Sin 2 Theta
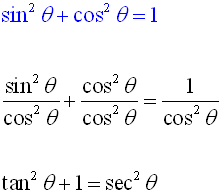



Pythagorean Identities Mathbitsnotebook Ccss Math
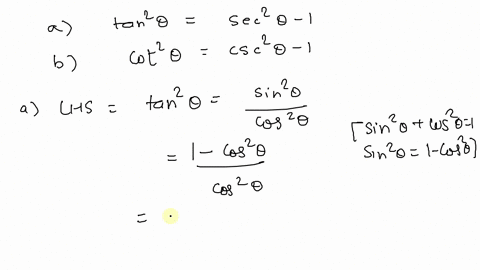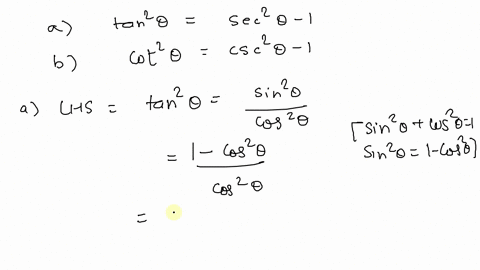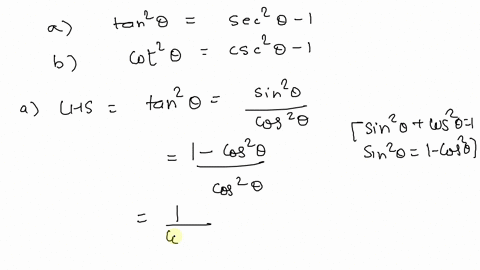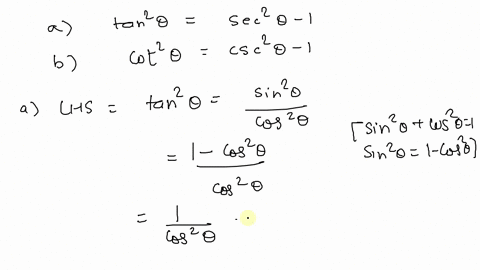



Solved Prove The Following Identities Tan 2 Theta 1 Sec 2 Theta



How Do You Verify Tan 28 Sin 28 Tan 28sin 28 Socratic
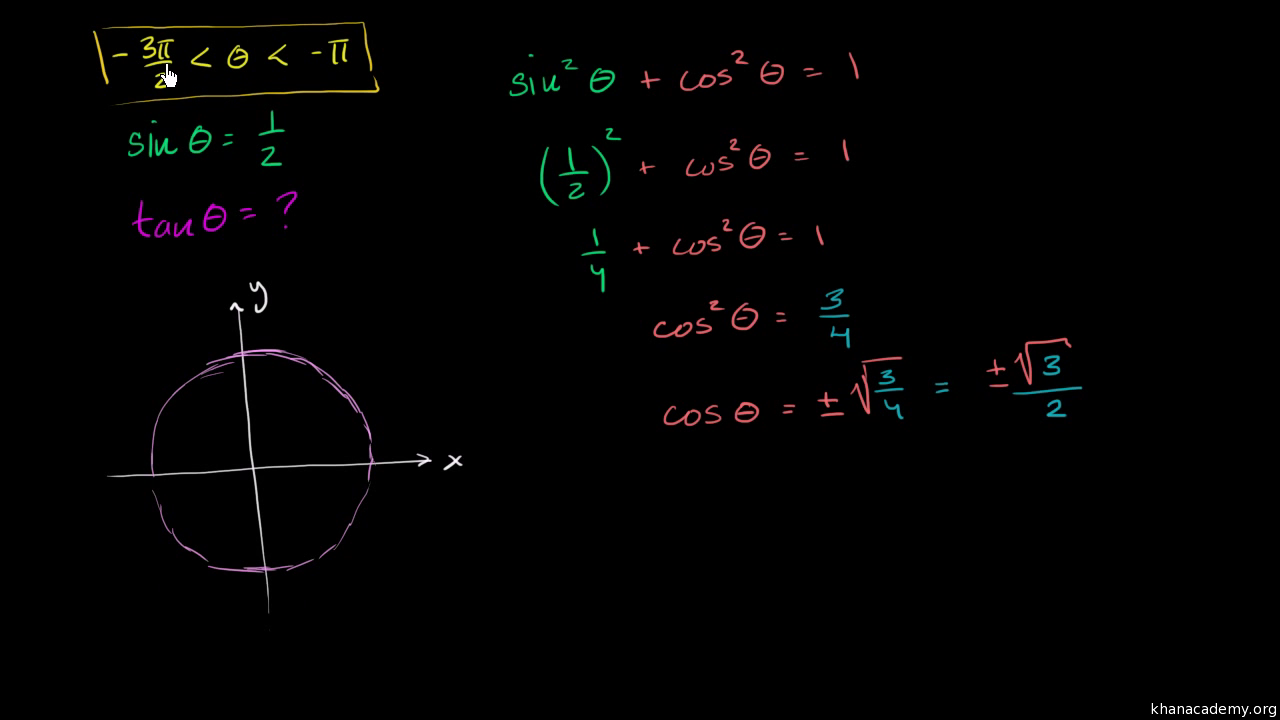



Using The Pythagorean Trig Identity Video Khan Academy




Trigonometric Identities A Plus Topper




Art Of Problem Solving




Summary Of Trigonometric Identities




What Is The Integration Of Tan 2x Solution Quora
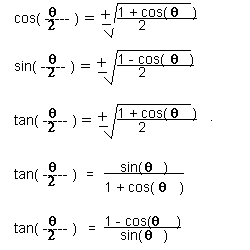



Double And Half Angle Formulas



3




Solved Does Tan 2 Theta Frac Sin 2 Theta Cos 2 Theta Justify Your Answer




Trigonometric Identities
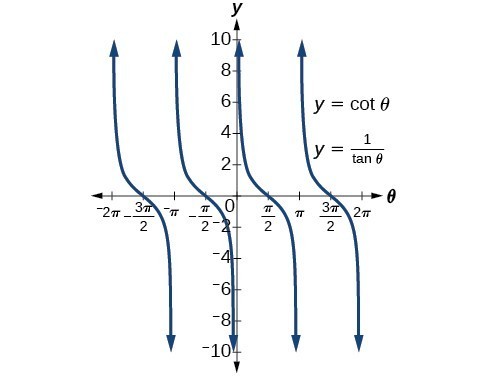



Solving Trigonometric Equations With Identities Precalculus Ii
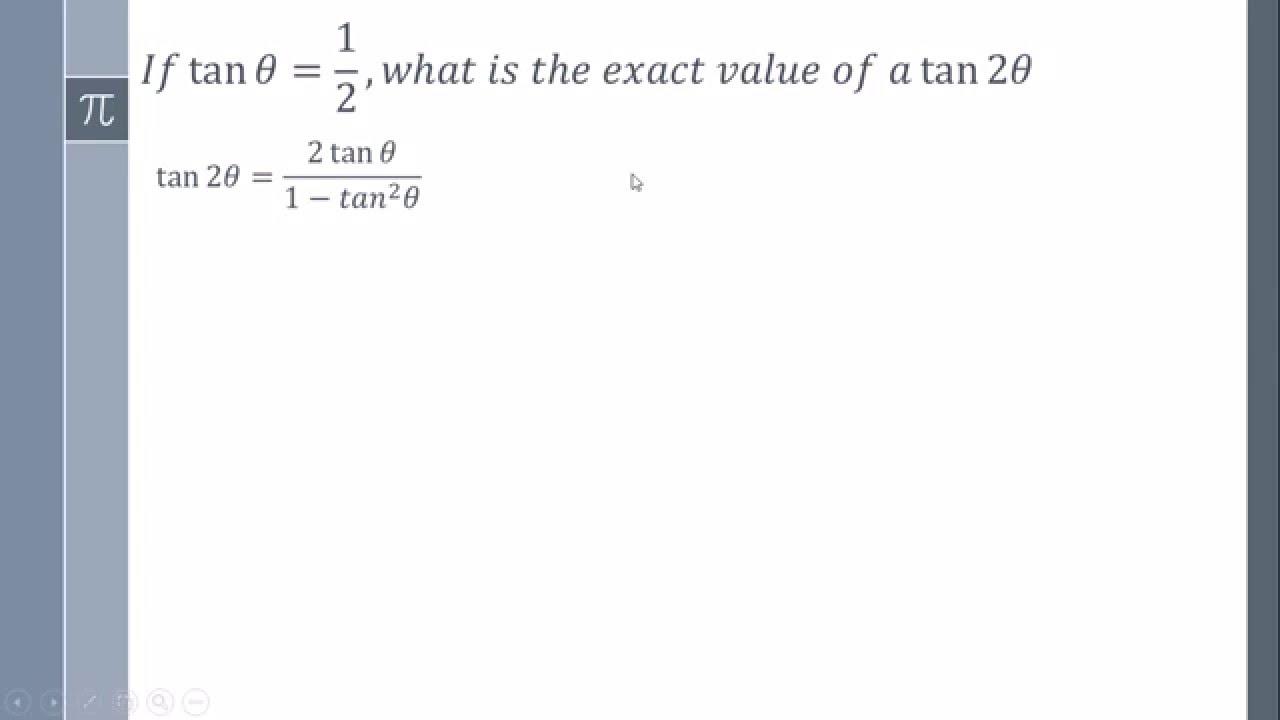



If Tan Of Theta Is 1 2 What Is The Exact Value Of Tan 2 Theta Youtube




Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions




Proof Tan 2 1 Sec 2 Youtube




Summary Of Trigonometric Identities




Tangent Identities




Prove Tan 3theta 1 Tan 2theta Cot 3theta 1 Cot 2theta



If Tan 8 2 Find The Values Of Other Trigonometric Ratios Sarthaks Econnect Largest Online Education Community




Understanding Pythagorean Identities Studypug



3
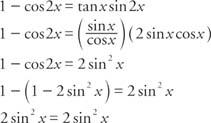



Double Angle And Half Angle Identities
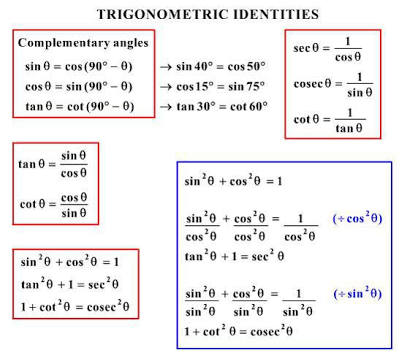



How Do You Simplify The Expression Sin 2theta Cos 2theta Cos 2theta Socratic




Solved Establish The Identity Tan 12 Theta 3 Tan 4 Chegg Com




Trigonometric Substitution Wikipedia
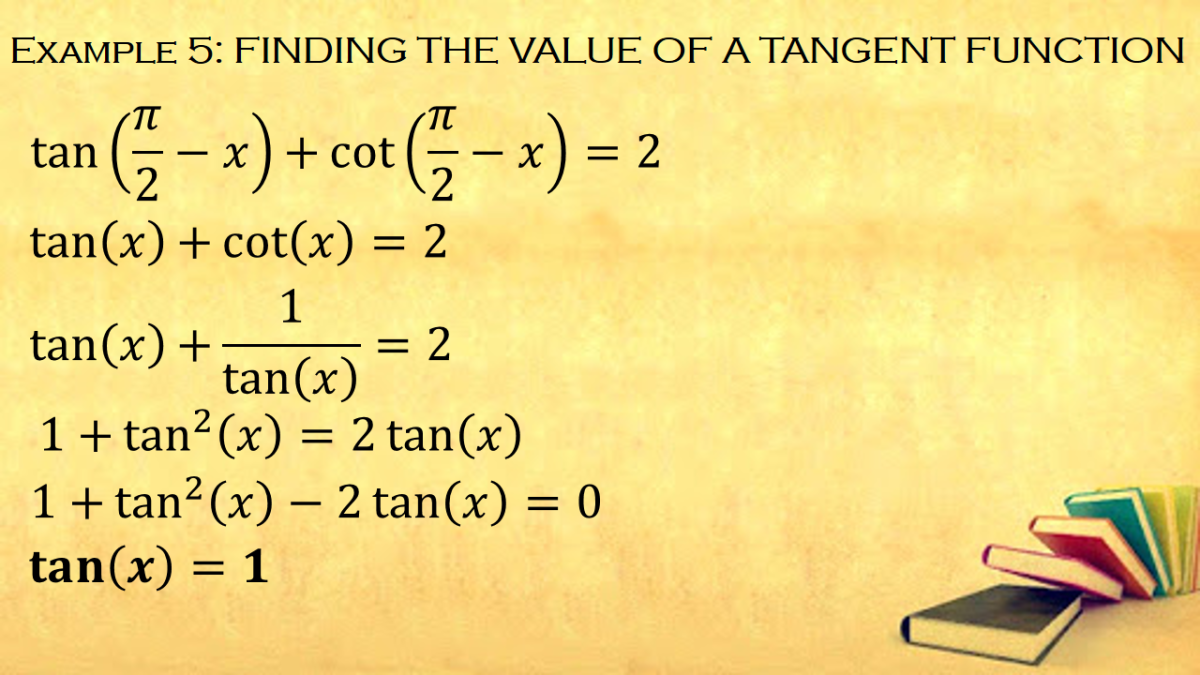



Cofunction Identities In Trigonometry With Proof And Examples Owlcation




Trigonometric Identities A Plus Topper




Solved Establish The Identity 1 Tan 2 Theta 1 Tan 2 Chegg Com



How I Remember Trig Identities Part 2 Beyond Solutions




If A 2 Sec 2 Theta B 2 Tan 2 Theta C 2 Prove That Sin Theta Plusmn Mathematics Topperlearning Com Q5azu9oo



0 件のコメント:
コメントを投稿